Geometria Analítica II

 1 - O uso do Determinante de terceira ordem na Geometria Analítica

1.1 - Área de um triângulo

Seja o triângulo ABC de vértices A(x_a , y_a) , B(x_b , x_c) e C(x_c , y_c) . A área S desse triângulo é dada por 
S = 1/2 . | D | onde ½ D½ é o módulo do determinante formado pelas coordenadas dos vértices A , B e C .

 Temos portanto: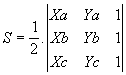

A área S é normalmente expressa em u.a. (unidades de área) 
Para o cálculo do determinante de terceira ordem, utilizamos a conhecida e prática regra de Sarrus.

1.2 - Condição de alinhamento de três pontos

Três pontos estão alinhados se são colineares , isto é , se pertencem a uma mesma reta .
É óbvio que se os pontos A , B e C estão alinhados , então o triângulo ABC não existe , e podemos pois considerar que sua área é nula ( S = 0 ) .
Fazendo S = 0 na fórmula de área do item 1.1 , concluímos que a condição de alinhamento dos 3 pontos é que o determinante D seja nulo , ou seja : D = 0 .

Exercício resolvido:

Se os pontos P(3 , 5) , Q(-3 , 8) e C(4 , y) são colineares , então o valor de y é :

a) 4
b) 3
c) 3,5
d) 4,5
e) 2

Solução: 

Para que estes pontos estejam alinhados (pontos colineares), deveremos ter: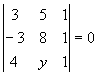

Desenvolvendo o determinante pela Regra de Sarrus, obtemos: 
- 32 - 3y + 15 + 24 - 3y + 20 = 0 \ y = 9/2 = 4,5. 
Portanto a alternativa correta é a letra D.

2 - Equação geral da reta.

Seja r a reta que passa pelos pontos A(x_a , y_a) e B(x_b , y_b). 
Seja P(x , y) um ponto qualquer desta reta . Pela condição de alinhamento de 3 pontos , podemos escrever: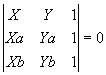

Desenvolvendo o determinante acima obtemos:
(Ya - Yb) . x + (Xa - Xb) . y + (XaYb - XbYa) = 0 .

Fazendo Ya - Yb = a , Xa - Xb = b e XaYb - XbYa = c , decorre que todo ponto P(x,y) pertencente à reta , deve verificar a equação :
ax + by + c = 0  
que é chamada equação geral da reta r .

Exemplos: 
2x + 5y - 4 = 0 (a = 2 , b = 5 , c = -4)
3x - 4y = 10 (a = 3 , b = -4 , c = -10); observe que podemos escrever 3x - 4y - 10 = 0.
3y + 12 = 0 (a = 0 , b = 3 , c = 12)
7x + 14 = 0 (a = 7 , b = 0 , c = 14)
x = 0 (a = 1 , b = 0 , c = 0) ordenadas .® equação do eixo Oy - eixo das 
y = 0 (a = 0 , b = 1 , c = 0) ® equação do eixo Ox - eixo das abscissas .

Observações:
a) a = 0 ® y = - c/b (reta paralela ao eixo dos x )
b) b = 0 ® x = - c/a (reta paralela ao eixo dos y)

3 - Posição relativa de duas retas

Sabemos da Geometria que duas retas r e s no plano podem ser :

Paralelas : r Ç s = Æ 
Concorrentes : r Ç s = { P } , onde P é o ponto de interseção .
Coincidentes : r = s.

Dadas as retas r : ax + by + c = 0 e s : a’x + b’y + c’ = 0 , temos os seguintes casos :

 ® as retas são coincidentes .

 ® as retas são paralelas .

as retas são concorrentes