Matrizes e Determinantes II
1 - Definições:
1.1 - Chama-se Menor Complementar ( D ij) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Podemos escrever: Da mesma forma determinaríamos D11, D12, D13, D21, D22, D31, D32 e D33. Faça os cálculos como exercício! 1.2 - Cofator de um elemento aij de uma matriz : cof ( aij ) = (-1 ) i+j . Dij . 2 - Teorema de Laplace 3 - Cálculo da inversa de uma matriz. a) A matriz inversa de uma matriz X , é a matriz X-1 , tal que X . X-1 = X-1 . X = In , onde In é a matriz identidade de ordem n. b) Matriz dos cofatores da matriz A: é a matriz obtida substituindo-se cada elemento pelo seu respectivo cofator. c) Fórmula para o cálculo da inversa de uma matriz: Onde: A-1 = matriz inversa de A;
Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :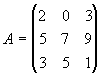
D23 = menor complementar do elemento a23 = 9 da matriz A . Pela definição, D23será igual ao determinante que se obtém de A, eliminando-se a linha 2 e a coluna 3, ou seja:![]()
Assim por exemplo, o cofator do elemento a23 = 9 da matriz do exemplo anterior, seria igual a:
cof(a23) = (-1)2+3 . D23 = (-1)5 . 10 = - 10.
Símbolo: cof A .![]()
det A = determinante da matriz A;
(cof A)T = matriz transposta da matriz dos cofatores de A .
Fim
